
Figure 10: Digital elevation model of the Upper Usumacinta region
With these considerations in mind the task then, was to devise a way to estimate the territorial extent of these polities. This in turn would be necessary for the definition of the boundary between the Pomoná and Piedras Negras kingdoms. Towards this end I worked on the premise that the effort involved in moving across the natural terrain would determine the size of a territory that can be effectively controlled and serviced by the centre. In a previous work (Anaya Hernández 2001) I presented in greater detail the model developed to estimate the territorial extent of the Usumacinta region polities, hence I refer the interested reader to this publication. Here I will limit myself to a brief review of the main stages involved in the creation of this model.

Figure 10: Digital elevation model of the Upper Usumacinta region
A series of topographic maps were digitised and a basic linear interpolation routine was performed to create the Digital Elevation Model (DEM) of the Upper Usumacinta River (Fig. 10). When estimating the effort of moving over the natural terrain two types of frictions have to be taken into account: isotropic and anisotropic. Isotropic friction refers to the friction that is equal in all directions, while the latter considers frictions that have both direction and magnitude, e.g. walking up or down a slope. To account for the first form of friction, digital maps for perennial and seasonal water bodies and the river network, which included the location of rapids and cascades, were digitised. Anisotropic friction was obtained by deriving the degree and direction of the slopes from the DEM. This resulted in a series of cost surfaces that reflect the effort of movement during the dry and rainy seasons, upstream and downstream, from each of the primary and subsidiary centres.
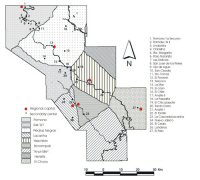
Figure 11: Initial territorial extent with secondary sites plotted
In turn the primary centre cost surfaces were used to estimate the areas that would be optimally covered from each major centre, by means of an allocation routine. The routine performs a spatial allocation algorithm based on a cost-distance surface where each cell is assigned to its nearest major centre. In this type of allocation algorithm, the feasible regions selected must be contiguous. A contiguous area consists of a group of spatial units (in this case the cells) that form a unit having an unbroken continuity, this meaning that it is possible to travel from any point to any other within the region without leaving the region (Diamond and Wright 1989). The result is a surface with identifiers that indicate to which major centre each cell is assigned to, obtaining in this way an initial territorial extent. The known secondary sites of the region were then plotted on this initial territory in order to note which primary centre could better service them (Fig. 11). The same allocation routine described above was run again but this time using the cost surfaces for both primary and subsidiary centres. In this manner the area optimally covered by each individual site was obtained. Finally in order to assemble the overall extent for the regional polities, these resulting areas were each assigned the identifier of the primary centre that laid closest to it (Fig. 12).
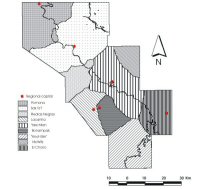
Figure 12: Final territorial extent of Upper Usumacinta polities
It is important to note that in the initial results of the allocation routine, the subsidiary sites of La Pasadita and El Chile fell within the territory of Yaxchilán; La Mar and El Cayo were contained within the territory of Piedras Negras; and Panhalé was included in the territory of Pomoná. This distribution is thoroughly supported by the inscribed monuments (Schele and Grube 1995) and lends a level of confidence to this approach.
© Internet Archaeology/Author(s)
University of York legal statements | Terms and Conditions
| File last updated: Tue Mar 7 2006