


Cite this as: de Gruchy, M., Caswell, E. and Edwards, J. 2017 Velocity-Based Terrain Coefficients for Time-Based Models of Human Movement, Internet Archaeology 45. https://doi.org/10.11141/ia.45.4
Intuitively, a person can think about how some terrains (paved path, dirt road) are easier to walk across than others (bog, loose sand). A computer model of human movement, however, needs to be informed of these differences through numbers called terrain coefficients, sometimes also called multipliers (Herzog 2014a). These terrain coefficients impose a penalty on movement through different terrains. Previous studies were conducted in the 1970s by a group of physiologists affiliated with the U.S. military, interested in the effect of land cover on energy consumption (Givoni and Goldman 1971; Soule and Goldman 1972; Pandolf et al. 1976; 1977). As a result, these studies have concentrated on calculating terrain coefficients for young adult males. Collectively, these studies calculated the terrain coefficients for walking across a total of nine different terrain types by measuring oxygen consumption to calculate differences in metabolic rate (see Herzog 2014a, table 3). Currently, computer models of human walking that factor terrain must rely on these values (presented here in Table 1), regardless of the population (male/female, old/young) or type of model employed (e.g. easiest route, fastest route). If a study involves movement across other terrains, then the values must be approximated by interpolating between the nine existing terrain coefficients. We had several questions: are terrain coefficients based on energy expenditure appropriate for models based on other variables (e.g. fastest routes)? Are terrain coefficients the same for males and females? Are they the same for different age groups? Does the burden of carrying extra weight (particularly important for migration) have a measurable impact on terrain coefficients?
| Terrain | Coefficient |
|---|---|
| Asphalt/blacktop | 1.0 |
| Dirt road | 1.1 |
| Grass | 1.1 |
| Light brush | 1.2 |
| Heavy brush | 1.5 |
| Swampy bog | 1.8 |
| Loose sand | 2.1 |
| Hard-packed snow | 1.6 |
| Ploughed field | 1.3 |
| (from Givoni and Goldman 1971; Soule and Goldman 1972; Pandolf et al. 1976; 1977; Yu et al. 2003; as summarised in Herzog 2014a) | |
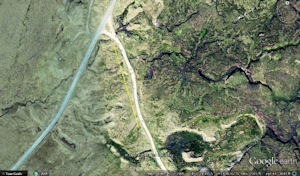
To help answer these questions, we measured the relative difficulty of traversing terrains through participants' velocities rather than oxygen consumption and metabolic rate, repeating four terrains from these original studies: blacktop/pavement, lawn grass, swampy bog, and loose sand. Additionally, we sought to expand the range of existing terrain coefficients by evaluating three new terrain types: a decayed asphalt/gravel path, tall grassland, and disturbed ground in an abandoned stone quarry. All seven terrains were located in County Durham and Tyneside, England (Figure 1), and selected using the authors' knowledge of the region combined with preliminary site reconnaissance to assess the suitability of each site.





We successfully recruited five male and five female participants across two broad age categories (20-35 and 36-50 years old) who participated for two days each across a total of six study days. All volunteered and provided informed consent. Durham University's archaeology and anthropology ethics committees reviewed and approved the project. The project's sample size is comparable to previous studies, which included between 6 and 14 subjects (Givoni and Goldman 1971; Soule and Goldman 1972; Pandolf et al. 1976). To avoid the possibility of fatigue artificially increasing the value of a terrain coefficient, subjects were provided time to rest with lawn chairs, and access to free tea and biscuits. We measured 200m-long routes with a 30-metre tape measure and marked it with bright orange flags placed every 10m. Variance in path location between days was less than 25cm. The participants then walked the path one at a time in isolation at the pace that they found most comfortable. The time they took to complete the total 200m and the final 100m were recorded to the nearest hundredth of a second using handheld stopwatch apps on an Apple iTouch 4.0 and an Android (5.0) phone (see spreadsheet).
Participants were given no guidance on how to proceed along the flagged paths except the suggestion that they take the route they found most comfortable while remaining within the terrain zone. Participants then repeated walking one at a time along the marked path with a weighted backpack equal to 30 per cent of their body weight as measured to the nearest pound on the first day of participation. This proportion of weight was sufficient in the original studies to cause a significant difference in performance (Soule and Goldman 1972).
Each path was 200m long – an arbitrary length that enabled subjects to fall into their natural stride, but not so long that they would be tired when walking the third or fourth terrain in a single day. That subjects did walk at a natural stride is demonstrated by the consistency in their velocities between the first 100m and the second 100m. This was particularly pronounced on the loose sand, where participants were placed in the middle of the track and walked 100m to the starting point. On this terrain, participants' completion times were always equal to within a tenth of a second between the first and second 100m, indicating that 100m is sufficient for kinesthetic learning of a terrain and the development of a natural stride.
In three cases (tall grass, bog, and disturbed ground) finding a stretch of land with one consistent terrain type that remained level in an accessible area proved difficult. In these cases, a shorter stretch of land (100m or 50m) was chosen that could be walked forwards and backwards multiple times without obstruction (see Figure 1 showing routes mapped in Google Earth). On two occasions weather conditions of high winds and rain prevented some participants from completing the full range of terrain paths and our data analysis was adjusted accordingly.
Following previous studies, the terrain coefficient value for pavement/asphalt was designated 1.00 and all other terrain coefficients were calculated as ratios relative to this value (see, for example, Soule and Goldman 1972). For each terrain we simply calculated the proportional increase in the length of time it takes for each participant compared to their baseline time traversing the same distance on pavement.
The results show a statistically significant difference for all but one of the terrain coefficients (decayed asphalt/gravel path) compared to the baseline pavement value, which was artificially set to 1.00 in keeping with previous studies; however, the actual difference can be quite small (see Table 2). This represents the first of our conclusions, that different terrains have a significantly measurable impact on speed of transit.
| Terrain | Coefficient | p-value |
|---|---|---|
| Pavement (cement) | 1 | N/A |
| Lawn Grass | 1.03 | 0.0165 |
| Loose Beach Sand | 1.19 | <0.0001 |
| Disturbed Ground (former stone quarry) | 1.24 | 0.0003 |
| Tall Grassland (with thistle and nettles) | 1.35 | <0.0001 |
| Bog | 1.79 | 0.0002 |
| The coefficients representing the velocity at which participants traversed each terrain relative to their speed on pavement. Data were analysed using the one sample t-test to compare the mean of the participants' coefficients for each terrain against the reference value of 1.0 (normality was first verified with q-q plots). We have included the p-value of each test in the table to indicate statistical significance. | ||
It is also interesting to investigate the variation of the terrain coefficients of each surface with population variables such as age and sex, and to see whether the burden of extra weight carries a significant penalty for each topographic type. So for each terrain we compared the performance of participants grouped according to these variables, to determine whether there is variation in each terrain coefficient between the groups. This was achieved with a two-sample t-test (unequal sample sizes and variances) comparing the means of the coefficients of the groups against one another for each terrain type. We took a 95% significance level on a null hypothesis that the average terrain coefficient of each group is the same.
Across each terrain, comparison between groups of participants demonstrates that age is not a significant factor for relative ease of movement. The authors suggest this may be due to a lack of elderly participants, who are more likely to have joint problems like arthritis, or younger children unable to maintain a comparable pace to adults. Sex, however, can be significant (at the 95% level) depending on the terrain. In our study lawn grass was found to show a significant difference between the coefficients of men and women (men: 1.067, women: 1.002, p-value: 0.03). A possible reason for this may be found in a study by Saibene and Minetti (2003), who found that a soft surface allows for a longer stride; the short length of the lawn grass would also enable greater freedom of movement. It is, therefore, possible that the observed difference between men and women on lawn grass may be the result of longer stride lengths by the men (although this was not measured). Contrary to what was expected, walking with a weighted pack equal to 30 per cent of body weight did not cause a consistently significant difference. The only terrain for which it had a significant effect was the loose beach sand (weighted: 1.225, unweighted: 1.151 p-value: 0.02). Observation, however, suggests that absolute weight may be an important factor for certain terrain types. On the bog terrain, the two smallest participants were able to avoid sinking into the bog when unweighted by walking across moss patches without breaking the surface. Once weighted, the smallest participant broke through the moss patches and sunk into the bog. By contrast, the largest participant sunk deep enough without added weight to become stuck and (temporarily) lose their boots.
Comparison between the new, velocity-based terrain coefficients and the pre-existing, metabolic rate-based terrain coefficients highlights that the two are not interchangeable. In particular we were unable to fit a simple linear model between the two sets of coefficients. Significant differences in our study occur at the hundredth decimal point, so the penalty incurred in speed of walking upon different terrain types appears to be less severe than that associated with increased metabolic activity. Furthermore, we found the bog has a much higher terrain coefficient value than the loose sand, whereas the original study evaluating both bog and loose sand (Soule and Goldman 1972) found the reverse.
In terms of scope, there are still many (hundreds, thousands?) of terrain types that remain untested. Additionally, there are still no studies incorporating children, elderly adults, and people with physical conditions that cause differences in gait. This last point is extremely important given the prevalence of diseases like rickets and polio that affected people in the past, as well as conditions like arthritis that continue to affect people today, altering their skeletons and their gait.
There are a number of additional conclusions that can be drawn from these results. First, researchers should not use variables based on oxygen consumption or metabolic rate in models other than those based on energy consumption. Likewise, the terrain coefficients from this study based on velocity should only be used in models based on time (e.g. fastest routes). Second, that the original studies used only young male subjects may not be an issue, but this should be confirmed with more studies, given the significant difference in performance between male and female subjects on lawn grass. Furthermore, statistical significance occurs on such a narrow scale that a difference of as little as 1.8 seconds across 200m is significant at the 95 per cent level. Whether this statistically significant difference is meaningful in the real world will depend on the model and research question at hand. For example, does it matter in the real world that walking 5km through one terrain would take 1 hour while walking a parallel path through another terrain would take 1 hour 1 minute and 48 seconds? In what instances would a difference on that scale matter to a person? Undoubtedly, the answer to this question will be culturally specific and at least partially based on available time-measuring technologies. It is unlikely such a small difference, for example, would matter to a fourth millennium B.C. Mesopotamian for whom the concept of hours, minutes, and seconds are more than a thousand years away, and for whom all administration (including the rationing of workers) is calculated in days (Brown 2000; 2010; Englund 1988).
Two of the main aims of publishing this article were:
There are, however, still many more terrain coefficients to calculate. The World Wildlife Fund has identified 867 terrestrial biomes around the world (Olson et al. 2001). Ideally, both energy- and velocity-based terrain coefficients will be calculated for each unique surface of the Earth, so that researchers studying regions around the world will have appropriate terrain coefficients to use in their models. Generating these will require an enormous amount of research and it is hoped that by sharing our methodology, others will be able to calculate additional terrain coefficients. We will be launching a website (https://terraincoefficients.wordpress.com/) that will aim to collect and maintain a complete list of all known terrain coefficients.
These velocity-based terrain coefficients are complementary to the pre-existing terrain coefficients by Givoni and Goldman (1971), Soule and Goldman (1972), Pandolf et al. (1976), and Pandolf et al. (1977), which were summarised by Herzog (2014a). They will be utilised in the PhD theses of both de Gruchy (in prep.) and Caswell (in prep.).
Cite this as: Herzog, I. 2017 Referee Comment on Velocity-Based Terrain Coefficients for Time-Based Models of Human Movement, Internet Archaeology 45. https://doi.org/10.11141/ia.45.4.ref
In many archaeological studies assessing the impact of topography on past human movement, only weak arguments without validation for the weights assigned to different terrain features are given. Therefore a study presenting terrain coefficients relying on sound tests is most welcome though the range of applications in archaeological modelling is limited.
Data on human movement are mainly used for two different classes of archaeological models:
It is difficult to model routes taken for other reasons, such as a shepherd's path with his flock, a pilgrim path, a ceremonial road, or the route taken by refugees.
Are these models time-based? All examples given above not belonging to the two classes mentioned first are probably not time-based in a straightforward way, i.e. people do not try to reach the target location as fast as possible. Nevertheless, the routes chosen are influenced by the terrain cover but in a different way: for instance, the shepherd possibly prefers grass areas.
Archaeological studies often reconstruct routes used for economic purposes by least-cost paths (LCPs). The most popular slope-dependent cost functions applied are either time-based or rely on physiological data measuring the energy expenditure. Arguments for both approaches can be found in archaeological least-cost studies. In my view, energy expenditure is more important, because economic studies suggest that people worked less in prehistory than nowadays, whereas food was limited. But only sound data like that presented by de Gruchy et al. allows this assumption to be checked with respect to a past society.
If a route was in constant use for economic purposes, the vegetation was cleared either by repeatedly walking the path or by cutting the vegetation. Several prehistoric roads in wetlands have been recorded (e.g. the Eclipse track constructed by interwoven rods in Somerset, see Renfrew and Bahn 1996, 314-15). So for this class of paths, the path surfaces differed from that of the surrounding landscape (see also Herzog 2014a, section 5.3: 'Vegetation cover should be mainly considered in the context of path formation'). It might be more important to take the effort of building paths into account than the time needed to walk on walker-unfriendly terrain). For the reasons given above, velocity-based terrain coefficients for grass, light or heavy brush, swampy bog and ploughed fields are probably not appropriate for LCP calculations.
The site catchment is 'the area around a site that would have been exploited by the site's occupants' (Renfrew and Bahn 1996, 242). Renfrew and Bahn refer to a publication suggesting a radius of 1 hour's walk for a sedentary agricultural site and a radius of 2 hours' walk for hunter-gatherer sites. For movement of hunters and gatherers some of the terrain coefficients are important. But farmers replace the initial vegetation by pastures and ploughed fields, they mostly use paths and the arguments given above concerning LCPs apply. Moreover, in many past farming societies, the use of wheeled vehicles and pack animals had an impact on human movement.
For people moving into an unfamiliar region or foragers searching for food, the target location is not known in advance.
People may adopt a strategy like Lévy walks to find food, an appropriate target location for the night or for building a new farmstead. For a mathematical discussion of such strategies see Lewis et al. 2013. On these walks foragers probably try to avoid terrain that does not allow fast progress. So with a raster-based model for human expansion, the probability of an agent moving into a neighbouring raster cell can be computed based on the terrain coefficients. Mostly young, healthy and adventurous people walk away from their home to find a new place to live. Therefore focusing on this group of people seems appropriate. But it is quite difficult to reconstruct the vegetation cover of past times. Often, only estimates at a global scale are available (e.g. Romanowska 2015).
It is possible that the terrain coefficients can be used in non-archaeological models as mentioned in the summary of the article. For emergency planning in mountainous areas, data on the velocity of walking on trails, grassland, and forest is available elsewhere (Ciesa et al. 2014). However, non-archaeological applications are beyond the scope of this review.
The authors state that 'it is unlikely that the relationship between metabolic rate and velocity is linear even when terrain is held constant'. They also refer to the formula published by Pandolf et al. (1977) that shows a quadratic relationship between metabolic rate and velocity, whereas Givoni and Goldman (1971) present a formula suggesting an exponent of 1.65 for velocity.
Not all studies referred to in the caption of Table 1 agree on the terrain coefficient values: Givoni and Goldman (1971) tentatively propose the following terrain coefficients: hard-surface road 1.2 [Table 1: 1.0], ploughed field 1.5 [Table 1: 1.3], sand dunes 1.8 [Table 1: Loose sand 2.1] and hard snow 1.6 [Table 1: 1.3].
Lejeune et al. (1998) found that 'walking on sand requires 2.1 to 2.7 times more energy expenditure than does walking on a hard surface at the same speed', whereas the multiplier for running on sand is only 1.6. Please note that the formula presented by Givoni and Goldman (also used by Soule and Goldman) is the product of the terrain coefficient with a factor depending on weight, load, velocity, and slope, whereas the Pandolf et al. (1977) formula consists of a term depending on weight and load only (estimating the energy consumption of standing) plus the extra energy required for movement, and only the latter term is multiplied by the terrain coefficient. Considering the fact that energy expenditure of walking normally is only about 50% above that of the metabolism at rest (Saibene and Minetti 2003), the two formulas mentioned are quite different.
It is no surprise that walking on English lawn grass is nearly as fast as walking on pavement. A softer track allows a longer step (Saibene and Minetti 2003) and this compensates for any impedance by the low vegetation. But the grass cover found within a clearing in the forest or on meadows differs from lawn. The time-based terrain coefficient for grassland derived from the data given in Ciesa et al. (2014, table 6) is 1.1 (compared to walking on trails). With today's climatic conditions in European countries north of the Alps, (low) grassland normally grows during the summer time and reaches the state 'tall grassland' in autumn if it is not cut. So to model the movement of hunters or gatherers in areas covered by grassland, often the seasons have to be taken into account. Ainslie et al. (2002) measured time, heart rate, energy consumption, temperature and many other values for a group of 11 subjects on a hill walk covering 12km. They report a large range for the duration of the hill walk (245-490 min), with a mean of 348 minutes. The reasons for increased time to complete the hill walk were mainly 'cold, wet, and windy weather and deep snow underfoot' (Ainslie et al. 2002, 182). This paragraph shows that the variability of most terrain factors is quite high.
The authors applied t-tests that require the assumption of normal distributions. So they check normality by q-q-plots. The quartiles given by Ciesa et al. (2014, table 6) suggest skewed distributions, and the authors of that publication apply a nonparametric test (Wilcoxon Mann–Whitney test) that does not require normal distributions.
The anonymised data used for computing the new time-based terrain coefficients was not available to the reviewer.
Additionally, it might be useful to measure the heart rate. From the heart rate, the weight of the participant and the distance covered, the calories burnt can be estimated. A stationary bicycle provides such an estimate. Small heart-rate monitors with low weight are affordable; carrying such a monitor most probably would not affect the results. Calculating the energy expenditure for walking a given distance must take both the increased heart rate and the velocity into account (cf. Ainslie et al. 2002).
The design of the study to generate the data and the results presented in this article are sound. The main issue is the problematic application of these data in archaeological research.
In archaeology, terrain coefficients are mainly important for modelling human expansion. But most projects dealing with such models cannot afford a detailed landscape reconstruction including the climatic conditions and the vegetation. Moreover, it is hard to estimate the impact of the time required to pass an unfamiliar piece of land on the choice of the route taken. Personally, after (temporarily) losing a boot, I would probably return and try another direction, if nothing forces me to walk on in that bog. Maybe some ethnographic sources are available dealing with this subject?
Due to the variability of the terrain coefficients found in previous studies and owing to varying climatic, seasonal and weather conditions, analysis of the impact of each terrain coefficient within its interval of variation is recommended rather than relying on one value only.
In my view the significance of this article is limited, if simply the data presented are considered. But if archaeologists do not just harvest the data but think thoroughly about the importance of these coefficients for their project, an important aim has been reached.
The limited range of terrain coefficients (energy- or time-based) remains an issue for studies of movement that factor terrain/land cover, and will remain an issue after the publication of this article. More terrain types need to be evaluated, results need to be replicated, and future studies should aim to utilise larger sample populations (more people).
As research into past mobility and routes develops, the need for robust terrain coefficients will only grow. For example, with the recent development of a means for quantitatively comparing a route model to a preserved or known historic/ancient route and for assessing the statistical significance of any overlap between the two (de Gruchy 2016), the possibility has emerged to extract information about travel practices in the past. It is known that travel practices, means of navigating and wayfinding, and even route choice are culturally informed. One might look at Bourdieu's original thesis on habitus, which included a case study on the correct way of walking for people in the Kabylia region of Algeria (Bourdieu 1977, 94); or contrast the results from wayfinding studies by Lewis (1976), who studied the Pintupi Aboriginals in Australia, with those by Widlok (1997; 2008) who studied the Hai//om in Namibia.
In quantitative route analysis, where the route model is merely a hypothesis meant to display how routes would look if people travelled according to a particular variable (easiest routes, fastest routes, shortest routes, etc.), statistically significant matches between the model and the preserved or known route signify the possibility that the modelled variable may have been important to the people who created and travelled the preserved/known, historic/ancient route.
This sort of analysis, however, is only as good as the model(s) underpinning it. If a model does not accurately and precisely express a route (fastest, easiest, etc.), then the risk of a statistical error in which a hypothesis is either falsely accepted or falsely rejected is high. For this reason, accounting for land cover is extremely important, as is the need for robust terrain coefficients. Research by Caswell (in prep.) has demonstrated that land cover may, in fact, be more important than slope as a cost factor in movement.
There are many existing assumptions about what variables were important to people travelling in the past (saving time or saving energy, to name two of the most common). It is time to move beyond assumptions. In her PhD thesis, de Gruchy (in prep.) has quantitatively compared route models to preserved routes/hollow ways to demonstrate that the fourth and early third millennium B.C. inhabitants and travellers through the North Jazira (Northern Syria and Iraq) often did not value any such physical variables at all. In fact, physical variables (easiest, fastest, and shortest) frequently did a worse job at predicting the preserved route locations than randomness. One of the conclusions, therefore, is that cultural variables took precedence.
Herzog raises important points about the application for terrain coefficients that we fully agree with. The first is that a route in constant use may be cleared of vegetation. Researchers must think critically about surfaces before applying terrain coefficients – the surface of a route may not match that of the surrounding landscape. In order to select the correct terrain coefficient (a type of natural landcover, a dirt road, a paved surface), it would be ideal if there were data on the frequency and density of traffic required to wear away the vegetation of different terrain types.
In de Gruchy's (in prep.) study area of the North Jazira, the routes are preserved as hollow ways, erosional features for which the terrain coefficient of a dirt road would certainly be more appropriate than one approximating a type of steppe – but only once enough people travelled the routes with sufficient frequency to erode away the vegetation and keep it eroded away. This point in time is difficult to date: settlement data suggest the routes were already in use during the early fourth millennium B.C. (Ur 2010, 99; de Gruchy in prep.); however the oldest artefact excavated to date from stratified fill of these hollow ways only dated to the third millennium B.C. (Wilkinson et al. 2010). It is unclear how much traffic would be required for a hollow way to form, although the recent formation of a new hollow way near Carchemesh on the Syrian/Turkish border between 2009 and 2012 suggests the process can take as little as three years or less, given a high enough volume of traffic (de Gruchy and Cunliffe forthcoming).
A second important point raised by Herzog (2014a) is the need to think about the technology employed by those who travelled. Currently, terrain coefficients are based on humans walking, not humans walking alongside a pack animal, not humans riding a horse or a camel, not humans riding a horse with a wagon in tow, not humans rowing, punting, or sailing a boat. It is expected that terrain coefficients will be different for each scenario.
Of course, an important prerequisite for applying terrain coefficients is knowledge of the contemporary land cover. Fortunately, there have been important developments that enable reconstruction of local land cover. Soto-Berelov et al. (2015) developed a top-down method that uses machine learning to reconstruct the former extents of present land cover types during earlier periods within the current climate, while de Gruchy et al. (2016) includes a bottom-up method for reconstructing land cover types (including land covers that may not exist in the present climate of a region) based on archaeobotanical data. So, in conclusion, in presenting the first time-based terrain coefficients, this article is very much a beginning, rather than an end. There is a lot more work to do.
Internet Archaeology is an open access journal based in the Department of Archaeology, University of York. Except where otherwise noted, content from this work may be used under the terms of the Creative Commons Attribution 3.0 (CC BY) Unported licence, which permits unrestricted use, distribution, and reproduction in any medium, provided that attribution to the author(s), the title of the work, the Internet Archaeology journal and the relevant URL/DOI are given.
Terms and Conditions | Legal Statements | Privacy Policy | Cookies Policy | Citing Internet Archaeology
Internet Archaeology content is preserved for the long term with the Archaeology Data Service. Help sustain and support open access publication by donating to our Open Access Archaeology Fund.